
Dr Sam Magellan
Dr Sam is a National Board Certified Doctor of Chiropractic and a Longtime resident of Northeast Arkansas. He graduated from Logan College of Chiropractic in 1995 and moved back to Jonesboro to serve the community in both his clinic and by becoming a community activist. He is deeply involved in the Jonesboro Lions Club and with the Jonesboro Chamber of Commerce Community Outreach Program. Dr Sam specializes in helping his patients treat their headaches and low back pain through the use of Chiropractic care as well as home management.
Our Team
Front Desk Manager
Sarah Masters

Hello how are you
Chiropractic Assistant
Jessica Longe

Licensed Massage Therapist
Elizabeth Sanders

Headaches

We can help you to decrease the frequency and severity of your headaches using our powerful headache treatment program.
Neck Pain

Neck pain is a common symptom that we see caused by the increased use in cellphones and personal computers. The good news is that we can help you treat it fast and get you longterm relief.
Low Back Pain

We can help you beat Low Back Issues and the associate pain by using our powerful Low Back Pain Protocol.
Why Choose our Office?
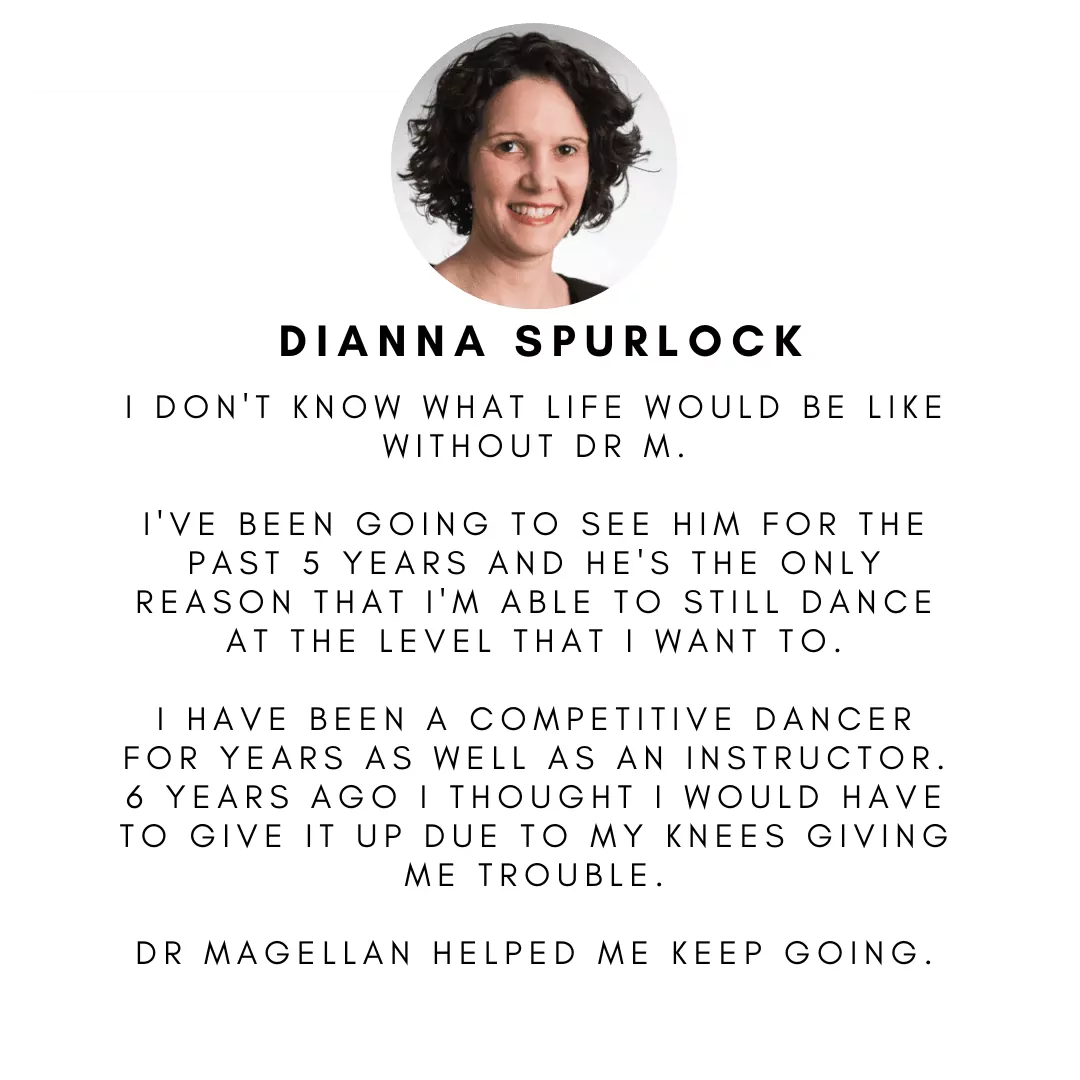
Let our Patients Tell You Why They Did.











Magellan Chiropractic Office Hours
Monday8AM-5PM | Tuesday8AM-5PM | Wednesday8AM-5PM | Friday8AM-5PM | Saturday9AM-12PM |
